Posts Tagged ‘maths’

Formules mathématiques dans WordPress : MathJax

Saturday, March 3rd, 2012

Quelques uns de mes articles nécessitent de représenter des formules mathématiques.

Jusqu’ici, j’avais utilisé la seule solution que je connaissais : le site LaTex Equation Editor for Writing Maths on the Internet !

Le principe est simple : la formule mathématique à afficher est une image, générée à la volée par ce site, en fonction d’une formule décrite selon la syntaxe de LaTex. L’avantage de cette méthode est qu’elle fonctionne dans tous navigateurs.

Le désavantage est que la qualité de l’image est discutable et nécessite un accès au site mentionné plus haut pour que l’affichage de l’article soit correct.

MathJax

C’est tout à fait par hasard que je suis tombé sur MathJax et plus particulièrement le plug-in MathJax-Latex. Il permet d’afficher une formule mathématique, décrite dans la syntaxe de LaTex, sous forme textuelle :

L’avantage de la forme textuelle est qu’elle supporte bien le zoom et permet d’être copier-coller. MathJax propose même un menu contextuel permettant un copier-coller plus performant.

La syntaxe est simple, il suffit de placer la formule entre les balises [latex] et [/latex]. Ainsi :

[latex]\sum_{k=1}^{n}k^{2}=\frac{n(n+1)(2n+1)}{6}[/latex]

affichera le résultat suivant :

Si le résultat est trop petit, ajouter \large en début de formule :

[latex]\large\sum_{k=1}^{n}k^{2}=\frac{n(n+1)(2n+1)}{6}[/latex]

Le résultat sera le suivant :

Il est également possible de placer la formule entre les délimiteurs $$. Par exemple :

$ $\sum_{k=1}^{n}k^{2}=\frac{n(n+1)(2n+1)}{6}$ $

Ce qui donne :

$$\sum_{k=1}^{n}k^{2}=\frac{n(n+1)(2n+1)}{6}$$

Attention : si vous avez installé le plug-in Jetpack, il faut désactiver l’extension latex.  Sinon, les formules placées entre les balises [latex] seront affichées sous forme d’images.

Tags:,
Posted in Divers | 1 Comment »

Mandelbrot

Saturday, February 18th, 2012

L’ensemble de Mandelbrot est une fractale bien connue pour son aspect si particulier en forme de cardioïde :

Cet ensemble est défini selon une formule relativement simple que nous verrons plus loin. Mais comme cette formule fait intervenir les nombres complexes, un petit rappel ne fera pas de mal.

Les nombres complexes

Si l’on se limite à l’ensemble des nombres réels (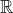R), il est impossible de calculer la racine carrée d’un nombre négatif, comme par exemple .

L’ensemble des nombres complexes () permet de résoudre ce genre de problème. L’idée est de nommer le résultat de par la lettre i. Cette lettre représente la partie imaginaire du nombre. Ainsi :

$$\sqrt{-16}=\sqrt(-1\cdot 16)=\sqrt(-1)\cdot\sqrt(16)=i4$$

On dit que i4 est la partie imaginaire d’un nombre. Rien n’empêche qu’un nombre complexe possède également une partie réelle. On note donc un nombre complexe sous la forme (a + ib), où a est la partie réelle et b la partie imaginaire.

Comme les nombres réels sont constitués de deux composantes (la partie réelle et la partie imaginaire), il est facile de les représenter graphiquement sur un plan. Par convention, la partie réelle du nombre est dessinée en abscisse et la partie imaginaire en ordonnée. Voici par exemple la représentation du nombre complexe (3 + i4) :

Plutôt que d’utiliser la forme (a + ib), il est également possible de représenter un nombre complexe par son module (la longueur du segment) et son argument (l’angle). On parle de notation polaire.

Le module, noté |z|, se calcule facilement au moyen du théorème de Pythagore :

$$|z|=\sqrt{a^{2}+b^{2}}$$

Opérations utiles

L’addition et la multiplication de nombres complexes est associative, commutative et distributive, au même titre qu’avec les nombres réels.

L’addition de deux nombres complexes (a+ib) et (a’+ib’) est une opération très simple :

$$(a + ib) + (a{}’ + ib{}’) = a+a{}’ + i(b+b{}’)$$

La multiplication de deux nombres complexes est une opération également relativement simple :

$$(a + ib) \cdot (a{}’ + ib{}’) = aa{}’ + aib{}’ + iba{}’ + i^{2}bb{}’$$

Comme i2= -1, on peut donc écrire :

$$(a + ib) \cdot (a{}’ + ib{}’) = aa{}’ – bb{}’ + i(ab{}’+a{}’b)$$

Pour représenter graphiquement l’ensemble de Mandelbrot, nous n’aurons pas besoin d’autres opérations.

L’ensemble de Mandelbrot

Un nombre complexe C fait partie de l’ensemble de Mandelbrot si la suite < ne tend pas vers l'infini (en module). . Il a été démontré en 1990 que cet ensemble a une dimension de Hausdorff de 2. Cela signifie que dès que le module de cette suite dépasse 2, c’est que le nombre en question ne fait pas partie de l’ensemble de Mandelbrot.

À savoir également que l’ensemble de Mandelbrot est compris entre les nombres complexes (-2.1 – i1.2) et (0.6 + i1.2).

Représentation de l’ensemble de Mandelbrot

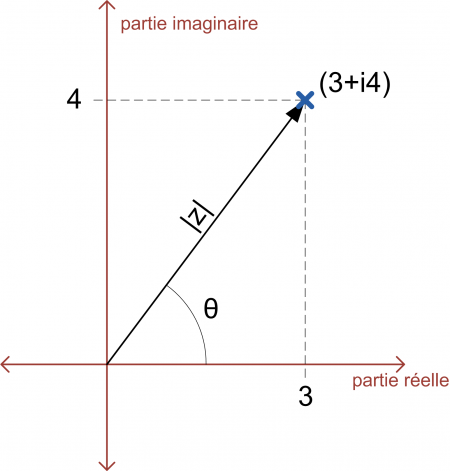
Pour afficher à l’écran l’ensemble de Mandelbrot, l’idée est d’associer à la surface de la fenêtre un intervalle de nombres complexes. Ainsi, chaque pixel de la fenêtre représente un nombre complexe pour lequel on pourra déterminer s’il appartient ou non à l’ensemble.

Il faut donc, pour chaque pixel de l’écran déterminer à quel nombre complexe il correspond, puis vérifier si ce nombre fait partie de l’ensemble de Mandelbrot. Si c’est le cas, le pixel sera affiché en noir. Sinon, il restera en blanc.

La plupart des langages de programmation ne permettent pas de manipuler en standard les nombres complexes. Toutefois, le calcul de la suite étant assez simple, il est facile de la calculer au moyen de nombres réels uniquement.

Posons et .

Calculons :

$$Z_{n+1}=Z_{n}\cdot Z_{n} + C=(Za_{n}+iZb_{n})\cdot (Za_{n}+iZb_{n}) + (Ca+ib)$$

$$Z_{n+1}=Za{_{n}}^{2}-Zb{_{n}}^{2}+i(2\cdot Za_{n} \cdot Zb_{n}) + Ca+iCb$$

Nous obtenons donc les calculs réels suivants :

$$Za_{n+1}=Z{_{na}}^{2}-Z{_{nb}}^{2}+Ca$$

$$Zb_{n+1}=2\cdot Za_{n} \cdot Zb_{n} + Cb$$

Reste à calculer cette suite pour déterminer si elle converge vers l’infini ou pas.

Nous avons vu plus haut que dès que le module de Z dépasse 2, il est certain que le nombre complexe en question ne fait pas partie de l’ensemble de Mandelbrot.

Il faut tester si le module est inférieur à 2 :

$$|z| < 2$$

Donc :

$$\sqrt{a^{2}+b^{2}} < 2$$

Nous pouvons simplifier le calcul en élevant les deux termes au carré :

$$a^{2}+b^{2} < 4$$

Par contre, si le nombre fait partie de l’ensemble, il faudrait calculer la suite à l’infini, ce qui n’est bien sûr pas réaliste. L’idée est donc de calculer les éléments de la suite jusqu’à un nombre d’itérations maximal, par exemple 200. Si après 200 itérations, le module de Z ne dépasse pas 2, on considère que la suite ne tend pas vers l’infini et que le nombre complexe fait partie de l’ensemble de Mandelbrot.

Il est donc impossible de dessiner cet ensemble de façon exacte. Sa représentation est une approximation dont l’exactitude dépend du nombre maximal d’itérations.

Algorithme

Voici l’algorithme permettant de vérifier si un nombre complexe C fait partie de l’ensemble de Mandelbrot :

procédure déterminant si C fait partie de l'ensemble de Mandelbrot
données : C : complexe
          Ca, Cb, Za, Zb, ZaTemp : réels
          Iteration, MaxIteration : entiers

début
   MaxIteration ← 200
   Ca ← partie réelle de C
   Cb ← partie imaginaire de C

   Za ← 0
   Zb ← 0

   Iteration ← 0

   tant que Za*Za + Zb*Zb < 4 et Iteration < MaxIteration faire
      ZaTemp ← Za*Za-Zb*Zb+Ca
      Zb ← 2*Za*Zb+Cb
      Za ← ZaTemp
      Iteration ← Iteration+1
   fin tant que

   si Iteration = MaxIteration alors
      le point fait partie de l'ensemble de Mandelbrot
   sinon
      le point ne fait pas partie de l'ensemble de Mandelbrot
   fin si
fin

Reste à utiliser cet algorithme pour dessiner quelque chose à l’écran. Il faut donc passer en revue chaque pixel de l’écran, déterminer à quels nombres complexes ils correspondent et les afficher s’ils appartiennent à l’ensemble de Mandelbrot.

Pour simplifier les choses, et comme l’ensemble de Mandelbrot est symétrique par l’abscisse, nous pouvons inverser l’orientation mathématique de l’axe imaginaire (l’ordonnée, axe vertical) afin qu’il soit dans la même direction que l’axe vertical d’affichage de l’écran.

procédure dessin de l'ensemble de Mandelbrot
données : LargeurEcran, HauteurEcran, Ligne, Colonne : entiers
          IntervalleComplexeGauche, IntervalleComplexeHaut,
          IntervalleComplexeDroite, IntervalleComplexeBas : réels
début
   IntervalleComplexeGauche ← -2.1
   IntervalleComplexeHaut ← 1.2
   IntervalleComplexeDroite ← 0.6
   IntervalleComplexeBas ← -1.2

   pour Ligne allant de 0 à HauteurEcran faire
      pour Colonne allant de 0 à LargeurEcran faire
         Ca ← Colonne * (IntervalleComplexeDroite - IntervalleComplexeGauche) / LargeurEcran + IntervalleComplexeGauche
         Cb ← Ligne * (IntervalleComplexeBas - IntervalleComplexeHaut) / HauteurEcran + IntervalleComplexeHaut

         si (Ca,Cb) fait partie de l'ensemble de Mandelbrot faire
            dessiner en Colonne, Ligne un point noir
         sinon
            dessiner en Colonne, Ligne un point blanc
         fin si
      fin pour
   fin pour
fin

 Implémentation en C++ avec Qt

Voici une implémentation simple en C++ et Qt des algorithmes présentés ci-dessus.

#include <QtGui/QApplication>

#include <QImage>
#include <QLabel>

const int IMAGE_WIDTH = 1024;
const int IMAGE_HEIGHT = 1024;

const int MAX_ITERATION = 200;

const unsigned int WHITE = 0x0FFFFFFFF;
const unsigned int BLACK = 0x0FF000000;

bool isInMandelbrotSet(double Ca, double Cb);

// Programme principal
int main(int ArgC, char *ArgV[]) {
    QApplication App(ArgC, ArgV);

    // Construit une image vide
    QImage Image(IMAGE_WIDTH, IMAGE_HEIGHT, QImage::Format_RGB32);
    Image.fill(WHITE);

    // Détermine l'intervalle à afficher
    QRectF ComplexArea(-2.2, -1.5, 3, 3);

    // Vérifie si les points font partie de l'ensemble de Mandelbrot
    for (int Line = 0; Line < IMAGE_HEIGHT; ++Line) {
        for (int Col = 0; Col < IMAGE_WIDTH; ++Col) {
            double Ca = Col * ComplexArea.width() / IMAGE_WIDTH + ComplexArea.left();
            double Cb = Line * ComplexArea.height() / IMAGE_HEIGHT + ComplexArea.top();

            if (isInMandelbrotSet(Ca, Cb))
                Image.setPixel(Col, Line, BLACK);
        }
    }

    // Affiche l'image dans une fenêtre
    QPixmap MandelbrotPixmap = QPixmap::fromImage(Image);
    QLabel Label;
    Label.setWindowTitle("Mandelbrot");
    Label.setPixmap(MandelbrotPixmap);
    Label.setMinimumSize(IMAGE_WIDTH, IMAGE_HEIGHT);
    Label.show();

    return App.exec();
}

// Détermine si le nombre complexe défini par Ca+iCb fait
// partie de l'ensemble de MandelBrot.
bool isInMandelbrotSet(double Ca, double Cb) {
    double Za = 0;
    double Zb = 0;

    int Iteration = 0;

    while (Za*Za + Zb*Zb < 4. && Iteration < MAX_ITERATION) {
        double ZaTemp = Za * Za - Zb * Zb + Ca;
        Zb = 2. * Za * Zb + Cb;
        Za = ZaTemp;
        ++Iteration;
    }

    return Iteration == MAX_ITERATION;
}

Et voilà le résultat :

Représentation colorée

Si vous avez déjà vu des représentations de l’ensemble de Mandelbrot, vous serez sans doute déçus par le résultat austère, noir et blanc, obtenu.

Toutefois, la représentation ci-dessus est conforme à la donnée mathématique : les points noirs sont ceux qui font partie de l’ensemble de Mandelbrot.

Par contre, ce qui est intéressant, ce sont les points qui ne font pas partie de l’ensemble. Au bout d’un certain nombre d’itérations, ces points sont exclus. L’idée est alors de leur donner un couleur, différente selon le nombre d’itérations qu’il a fallu pour les exclure.

Solution simple

Un ordinateur est capable de recréer des millions de couleurs en mélangeant (synthèse additive) les trois couleurs primaires rouge, vert et bleu.

Pour chaque couleur primaire, il est possible de donner une intensité comprise en zéro (noir) et 255 (couleur vive).

Nous pourrions donc fixer à 256 le nombre maximal d’itérations dans notre algorithme. Dès lors, il suffit d’utiliser directement le nombre d’itérations obtenu comme intensité d’une des couleurs de base, par exemple le rouge.

Si le nombre maximal (256) est atteint le point sera dessiné en noir.

Le programme doit être modifié de telle sorte que la méthode isInMandelbrotSet() retourne un paramètre supplémentaire contenant le nombre d’itérations.

#include <QtGui/QApplication>

#include <QImage>
#include <QLabel>

const int IMAGE_WIDTH = 1024;
const int IMAGE_HEIGHT = 1024;

const int MAX_ITERATION = 256;

const unsigned int WHITE = 0x0FFFFFFFF;
const unsigned int BLACK = 0x0FF000000;

bool isInMandelbrotSet(double Ca, double Cb, int* pIterationCount = 0);

// Programme principal
int main(int ArgC, char *ArgV[])
{
    QApplication App(ArgC, ArgV);

    // Construit une image vide
    QImage Image(IMAGE_WIDTH, IMAGE_HEIGHT, QImage::Format_RGB32);
    Image.fill(WHITE);

    // Détermine l'intervalle à afficher
    QRectF ComplexArea(-2.2, -1.5, 3, 3);

    // Vérifie si les points font partie de l'ensemble de Mandelbrot
    for (int Line = 0; Line < IMAGE_HEIGHT; ++Line) {
        for (int Col = 0; Col < IMAGE_WIDTH; ++Col) {
            double Ca = Col * ComplexArea.width() / IMAGE_WIDTH + ComplexArea.left();
            double Cb = Line * ComplexArea.height() / IMAGE_HEIGHT + ComplexArea.top();

            int Iteration = 0;
            if (isInMandelbrotSet(Ca, Cb, &Iteration))
                Image.setPixel(Col, Line, BLACK);
            else
               Image.setPixel(Col, Line, Iteration*256*256);
        }
    }

    // Affiche l'image dans une fenêtre
    QPixmap MandelbrotPixmap = QPixmap::fromImage(Image);
    QLabel Label;
    Label.setWindowTitle("Mandelbrot");
    Label.setPixmap(MandelbrotPixmap);
    Label.setMinimumSize(IMAGE_WIDTH, IMAGE_HEIGHT);
    Label.show();

    return App.exec();
}

// Détermine si le nombre complexe défini par Ca+iCb fait
// partie de l'ensemble de MandelBrot.
bool isInMandelbrotSet(double Ca, double Cb, int* pIterationCount) {
    double Za = 0;
    double Zb = 0;

    int Iteration = 0;

    while (Za*Za + Zb*Zb < 4. && Iteration < MAX_ITERATION) {
        double ZaTemp = Za * Za - Zb * Zb + Ca;
        Zb = 2. * Za * Zb + Cb;
        Za = ZaTemp;
        ++Iteration;
    }

    if (pIterationCount)
       *pIterationCount = Iteration;
    return Iteration == MAX_ITERATION;
}

Voilà le résultat obtenu :

Il y a sans doute moyen de faire mieux !

Le problème vient du fait que la surface éloignée de l’ensemble de Mandelbrot est très sombre, car il faut peu d’itérations pour déterminer que ces points ne font pas partie de l’ensemble.

Par contre, pour les points proches de la frontière de l’ensemble, les variations du nombre d’itérations sont plus marquées, mais le choix des couleurs ne rend pas compte de cette diversité.

Solution avancée

La meilleure solution est donc de mettre au point un dégradé de couleurs. Toute la difficulté sera de choisir judicieusement les couleurs constituant ce dégradé.

Voici un dégradé possible :

Les couleurs clés sont les suivantes :

Position Couleur R V B Hexadécimal
0 % rouge foncé 128 0 0 800000h
20 % jaune 255 255 0 FFFF00h
40 % orange 255 165 0 FFA500h
60 % pourpre 160 32 240 A020F0h
80 % bleu nuit 25 25 112 191970h
100 % rouge foncé 128 0 0 800000h

Et voilà le résultat correspondant :

Le rendu est bien plus satisfaisant !

La principale difficulté consiste donc à programmer le dégradé de couleur, en particulier en ce qui concerne les couleurs intermédiaires.

Pour ce faire, le plus simple est de coder une classe capable de gérer un dégradé entre certaines couleurs clé.

Le code étant trop long pour être affiché sur cette page, il peut être téléchargé : Projet Qt : MandelBrotGUI

À la découverte de la fractale

La partie amusante peut maintenant commencer : changer l’intervalle affiché afin d’admirer de magnifiques figures fractales.

C’est la ligne suivante qui détermine l’intervalle qui sera affiché :

    // Détermine l'intervalle à afficher
    QRectF ComplexArea(-2.2, -1.5, 3, 3);

Le premier nombre indique la limite gauche de l’intervalle (-2.2). Le deuxième nombre, sa limite haute (-1.5). Les deux derniers nombres indiquent la largeur et la hauteur de l’intervalle (3). Pour un affichage dans une fenêtre carrée, il faudrait que la largeur et la hauteur soient identiques.

Observons ce que l’on obtient avec les valeurs suivantes : -0.83, -0.21, 0.05, 0.05. La ligne de code devient QRectF ComplexArea(-0.83, -0.21, 0.05, 0.05);

Lissage des couleurs

Cette vue spectaculaire souffre toutefois encore d’un petit défaut : le dégradé de couleurs présente un effet d’escaliers. C’est la conséquence d’utiliser directement le nombre d’itérations pour obtenir une couleur, qui est un nombre entier. Le résultat est donc discret (à l’opposé de continu), ce qui provoque  dans certaines situations ces escaliers disgracieux.

Pour y remédier il existe différents algorithmes dont le normalized iteration count*. Il permet de calculer une variation décimale du nombre d’itérations pour obtenir un dégradé plus fin.

La formule est la suivante :

$$n+\frac{\log (\log b)-\log(\log \left | Z_{n} \right |)}{\log 2}$$

où n est le nombre d’itérations et b le rayon de sortie (qui correspond à la dimension de Hausdorff et qui vaut donc 2 dans notre cas).

L’amélioration est nette :

Essayons d’autres valeurs : -0.749, -0.177488, 0.02, 0.02. La ligne de code devient QRectF ComplexArea(-0.749, -0.177488, 0.02, 0.02);

Nombre d’itérations

Nous avons vu plus haut que pour déterminer si un nombre fait partie de l’ensemble ou pas, il faudrait théoriquement calculer la suite à l’infini. Une approximation est donc réalisée en limitant le nombre d’itérations effectué lors du calcul de la suite.

Le problème d’une telle approximation, c’est que lorsqu’on veut afficher des détails, elle a un impact direct sur la précision obtenue.

Voici, pour les valeurs -0.726277, -0.257609, 0.000332257, 0.000332257 le résultat avec une limite de 256 itérations :

La cardioïde est passablement déformée. Voici une meilleure approximation avec une limite de 512 itérations :

Avec une limite de 1024 itérations :

Et enfin avec une limite de 2048 itérations :

Toute la difficulté revient à trouver une limite qui donne de bons résultats, en un temps acceptable !

Sources :

Wikipédia : Ensemble de Mandelbrot

Wikipedia : Mandelbrot set

Coloring dynamical systems in the complex plane, Garcia, Fernandez, Barrallo, Martin

Tags:, ,
Posted in Développement | 2 Comments »

Vitesse moyenne

Saturday, January 14th, 2012

Voici un petit problème physico-mathématique que j’ai trouvé très intéressant.

L’énoncé est très simple :

Une voiture se déplace d’un point A à un point B à la vitesse constante de 10 km/h.
À quelle vitesse (toujours constante) doit-elle rouler, en revenant du point B jusqu’au point A, pour que sa vitesse moyenne soit de 22 km/h ?


Photo de Ian Britton, obtenue de www.freefoto.com.

Avant de continuer de lire, essayez de trouver la réponse !

Première solution

Vous avez peut-être obtenu comme réponse 34 km/h, sans être franchement convaincu de la justesse du résultat ?

En faisant une simple moyenne arithmétique, on obtient effectivement 34 km/h.

$$v_{moyenne} = \frac{v_{aller} + v_{retour}}{2}$$

$$v_{moyenne} = \frac{v_{aller} + v_{retour}}{2}$$

$$v_{retour} = 2\cdot v_{moyenne}-v_{aller} = 2\cdot 22-10=34\, km/h$$

Le problème avec cette solution est qu’elle ne tient pas compte du temps. Si la voiture avait roulé autant de temps à 10 km/h qu’à 34 km/h, sa moyenne serait effectivement 22 km/h.

Mais, en roulant à 10 km/h le long de la distance AB, elle va passer plus de temps à cette vitesse qu’en revenant depuis le point B.

Deuxième solution

Dès lors, il faut réécrite notre équation en tenant compte du temps. Pour ce faire, rappelons la formule de base pour le calcul d’une vitesse :

$$vitesse = \frac{distance}{temps}$$

Dès lors, le temps pour parcourir une distance se calcule ainsi :

$$temps = \frac{distance}{vitesse}$$

Soient et les vitesses d’aller et de retour et la distance entre le point A et le point B.

Soit le temps passé pour aller du point A au point B :

$$t_{aller} = \frac{AB}{v_{aller}}$$

Soit le temps passé pour aller du point B au point A :

$$t_{retour} = \frac{AB}{v_{retour}}$$

$$v_{moyenne} = \frac{distance\,totale}{temps\,total} = \frac{2\cdot AB}{t_{aller} + t_{retour}}=\frac{2\cdot AB}{\frac{AB}{v_{aller}}+\frac{AB}{v_{retour}}}$$

$$v_{moyenne} = \frac{2\cdot AB}{\frac{AB\cdot v_{retour}}{v_{aller}\cdot v_{retour}}+\frac{AB\cdot v_{aller}}{v_{retour}\cdot v_{aller}}}=\frac{2\cdot AB\cdot v_{aller}\cdot v_{retour}}{AB\cdot (v_{aller}+v_{retour})}=2\cdot\frac{v_{aller}\cdot v_{retour}}{v_{aller}+v_{retour}}$$

À partir de cette dernière formule, retrouvons celle permettant de calculer la vitesse retour :

$$v_{moyenne}\cdot v_{aller} + v_{moyenne}\cdot v_{retour} = 2\cdot v_{aller}\cdot v_{retour}$$

$$v_{moyenne}\cdot v_{retour} – 2\cdot v_{aller}\cdot v_{retour} = -v_{moyenne}\cdot v_{aller}$$

$$v_{retour} (v_{moyenne} – 2 v_{aller}) = -v_{moyenne}\cdot v_{aller}$$

$$v_{retour}=-\frac{v_{moyenne}\cdot v_{aller}}{v_{moyenne} – 2 v_{aller}}$$

Il ne nous reste plus qu’à résoudre la formule avec des valeurs numériques :

$$v_{retour}=-\frac{22\cdot 10}{22 – 2\cdot 10}=-\frac{220}{2}=-110\,km/h$$

Voilà un résultat pour le moins surprenant ! Est-ce qu’il indique une erreur ? Vérifions notre calcul :

$$v_{moyenne} =2\cdot\frac{v_{aller}\cdot v_{retour}}{v_{aller}+v_{retour}}=2\cdot\frac{10\cdot -110}{10+(-110)}=\frac{-2200}{-100}=22\,km/h$$

Il faut se rendre à l’évidence : notre calcul est mathématiquement parfaitement juste ! Par contre, il est physiquement irréalisable !

Explication

Cela peut être expliqué de la façon suivante : si à l’aller, notre vitesse moyenne est de 10 km/h, cela signifie qu’en une heure, nous avons parcouru 10 kilomètres. Si nous avions la possibilité de revenir instantanément à notre point de départ, nous aurions alors parcouru, en une heure, 20 kilomètres (l’aller-retour), ce qui donne une vitesse moyenne de 20 km/h.

En clair, il est impossible de faire plus que doubler sa vitesse moyenne.

Pour illustrer cela différement, dessinons la courbe de notre fonction :

On voit que la courbe pour une vitesse de retour positive tend vers 20 km/h.

Ceci peut être également démontré au moyen des limites.

$$v_{moyenne} =2\cdot\frac{v_{aller}\cdot v_{retour}}{v_{aller}+v_{retour}}$$

Si l’on note v pour la vitesse de retour :

$$\lim\limits_{v \to \infty} 2\cdot\frac{v_{aller}\cdot v}{v_{aller}+v}=2\cdot v_{aller}$$

La limite confirme donc ce que l’on a vu plus haut.

Conclusion

Nous avons vu lors de la première solution que la moyenne arithmétique n’est pas adaptée à ce genre de problème.

Dans notre situation, c’est la moyenne harmonique qu’il faut utiliser.

À noter que si vous avez des notions de base d’électrotechnique et plus particulièrement de calculs de circuits de résistances, vous avez déjà utilisé, peut-être sans le savoir, la moyenne harmonique pour calculer un couplage parallèle de résistances.

Tags:
Posted in Divers | Comments Closed

Calculs cycliques et modulo

Friday, December 16th, 2011

Le modulo

L’opération arithmétique modulo est souvent utilisée en informatique, et plus particulièrement dans le développement.

Elle est souvent présentée comme le reste d’une division entière. Par exemple :

7 ÷ 2 = 3 reste 1. Ainsi, 7 modulo 2 = 1.

27 ÷ 24 = 1 reste 3. Ainsi, 27 modulo 24 = 3.

C’est une opération qui se révèle très utile dès que l’on a affaire à des calculs cycliques, le plus connu étant le problème de l’horloge.

En effet, une horloge (digitale dans notre exemple) indique l’heure de la journée de façon numérique, les heures allant de 0 (minuit) à 23. Une heure après 23 heures, il est minuit. L’horloge recommence un cycle à zéro.

Il existe bien sûr d’autres exemples, ayant des cycles différents. Par exemple, une montre analogique a un cycle de 12 : lorsque l’aiguille a fait un tour complet, elle reprend à 1.


Les angles (en degrés) ont un cycle de 360, etc.

Calculs cycliques

Lorsque des calculs cycliques doivent être effectués, il faut tenir compte de la durée du cycle.

Par exemple, s’il est 10 heures et que l’on souhaite calculer l’heure qu’il sera dans 5 heures, il suffit de faire une addition : 10 + 5 = 15 heures.
Par contre, si il est 22 heures (et que l’on souhaite encore calculer l’heure qu’il sera dans 5 heures), la simple addition abouti à un résultat erroné : 22 + 5 = 27 heures.

Le problème vient du fait que toutes les 24 heures, l’horloge recommence à zéro. Elle travaille donc dans une arithmétique modulaire (cyclique) dont le cycle, nous l’avons vu, est de 24 heures.

L’opération arithmétique modulo permet de tenir compte du cycle. Ainsi, pour garantir que le résultat soit toujours conforme au cycle de 24 heures de l’horloge, il suffit d’appliquer un modulo à l’addition :

heure ultérieure = (heure actuelle + décalage) modulo 24.

En reprenant notre exemple :

heure ultérieure = (22 + 5) modulo 24 = 3

Ce qui est correct : 5 heures après 22 heures, il sera 3 heures du matin.

Maintenant, essayons de faire la même chose mais pour calculer une heure précédente.

Par exemple, s’il est 11 heures et que l’on souhaite calculer l’heure qu’il était il y a 7 heures, il suffit de faire une soustraction : 11 – 7 = 4 heures.
Par contre, s’il est 6 heures (et que l’on souhaite encore calculer l’heure qu’il était il y a 7 heures), la simple soustraction aboutit à un résultat erroné : 6 -7 = -1 heures. Ce n’est pas une surprise.

Dès lors, il semble logique qu’il faille appliquer la technique du modulo :

heure précédente = (heure actuelle – décalage) modulo 24.

ou selon notre exemple : heure précédente = -1 modulo 24.

Mais quel est le reste de la division de -1 par 24 ?

-1 ÷ 24 = 0 reste -1

C’est là que les problèmes commencent : dans le cas d’une arithmétique cyclique, le résultat attendu n’est pas -1 mais 23.

Cet exemple met en lumière que le reste d’une division entière et le modulo ne sont pas interchangeables :

  • Tant que les calculs sont effectués sur des nombres positifs, le reste de la division entière et le modulo donnent des résultats identiques.
  • Dès qu’un des nombres de la division est négatif, les deux opérations ne fournissent plus les mêmes résultats.

En résumé

Nous venons de voir que le modulo n’est pas une opération identique au reste de la division entière. Elle diffère en particulier lorsque le dividende et/ou le diviseur sont négatifs.

Voici un tableau récapitulatif :

Dividende Diviseur Quotient Reste Modulo
27 24 1 3 3
24 24 1 0 0
15 24 0 15 15
0 24 0 0 0
-1 24 0 -1 23

Reprenons la façon de calculer le reste d’une division :

La partie intéressante est l’arrondi : quel arrondi utiliser pour convertir le résultat de la division (un nombre réel) en un nombre entier ? Car il y a bien sûr plusieurs façons d’arrondir un nombre.

La réponse la plus évidente est de ne garder que la partie entière du résultat (c’est une troncature). Par exemple, la partie entière de 3.4 est 3. La partie entière de 4.9 est 4.

Il en résulte que la partie entière est toujours inférieure ou égale au nombre réel.

Qu’en est-il lorsque le résultat est négatif ?

Si l’on fait une troncature, la partie entière de -3.4 est -3. La partie entière de -4.9 est -4.

On constate qu’avec cette méthode le sens de l’arrondi change pour les nombres négatifs : les nombres arrondis sont supérieurs ou égaux aux nombres réels.

Une autre alternative serait alors d’arrondir le nombre réel au nombre entier inférieur (arrondi vers -∞). Ainsi, l’arrondi de -3.4 serait -4 et celui de -4.9 serait -5. Ainsi, peu importe que le nombre à arrondir soit positif ou négatif, son arrondi est toujours égal ou inférieur.

Il y a donc deux façons d’arrondir un nombre à virgule qui nous intéresse et qui donnerait des résultats corrects : soit en effectuant une troncature(arrondi vers zéro), soit en effectuant un arrondi vers -∞.

Ces deux façons de faire aboutissent au même résultat pour les nombres positifs, mais à des résultats différents pour les nombres négatifs.

C’est cette différence de méthode d’arrondi qui débouche soit sur le calcul d’un reste de la division (troncature), soit sur le modulo (arrondi vers -∞).

En résumé :

L’opérateur modulo en C++

Voyons maintenant comment réagit l’opérateur modulo en C++, symbolisé par le symbole % :

cout << 27 % 24 << "\n" // affiche 3
cout << -1 % 24 << "\n" // affiche -1

On voit que l’opérateur modulo (%) est mal nommé : il ne calcule pas le modulo, mais le reste de la division entière. Ceci provient du fait qu’en C++, la division entière utilise la troncature
pour convertir un résultat réel en entier.

Pour calculer le modulo en C++, il faut donc écrire notre propre fonction, qui utilisera un arrondi vers -∞ :

int modulo(int Dividende, int Diviseur) {
   return Dividende - std::floor(static_cast<double>(Dividende)/Diviseur) * Diviseur;
}

La fonction floor() (de la bibliothèque cmath) effectue un aarrondi vers -∞.

Le static_cast<double>() permet de forcer la division à être effectuée sur des nombres réels. Sans cela, la division retournerait directement un résultat entier (obtenu par troncature
) et la fonction floor() n’aurait plus aucun effet.

Par souci de clarté, on pourrait également écrire notre propre fonction calculant le reste de la division, en utilisant une troncature :

int remainder(int Dividende, int Diviseur) {
   return Dividende - Dividende/Diviseur * Diviseur;
}

Mais vous l’avez compris, cette fonction fait double emploi avec l’opérateur %.

Excel et VBA

Excel propose la fonction MOD(), qui calcule bel et bien le modulo.

Par contre, il faut faire attention à l’opérateur Mod de VBA, qui calcule, comme son nom ne l’indique pas, le reste !

Dividende Diviseur Quotient Reste Modulo Fonction Excel MOD() Opérateur VBA Mod
27 24 1 3 3 3 3
24 24 1 0 0 0 0
15 24 0 15 15 15 15
0 24 0 0 0 0 0
-1 24 0 -1 23 23 -1

C’est bien beau, mais à quoi ça sert ?

Voici un exemple concret qui illustre bien l’intérêt de comprendre la différence entre le reste et le modulo. Nous allons réaliser un petit programme de codage/décodage au moyen du chiffre de César.

Le chiffre de César est une méthode de chiffrement très simple (et peu robuste). Elle consiste à remplacer chaque lettre d’une phrase par une lettre à distance fixe dans l’ordre de l’alphabet. Par exemple, avec un décalage de 3, la lettre A devient D, la lettre J devient M, etc.

Ainsi, la phrase BONJOUR LES AMIS, avec un décalage de 3, deviendra ERQMRXU OHV DPLV !

Pour implémenter dans un langage informatique cette méthode de chiffrement, il faut au préalable numéroter chaque lettre (lui donner un numéro), afin de pouvoir faire le calcul du décalage.

Lors du calcul du décalage, il faut tenir compte de l’aspect cyclique de la numérotation des lettres de l’alphabet : après la lettre Z (qui a le numéro 25), il faut reprendre à la lettre A (qui a le numéro 0). Cette difficulté est contournée par l’utilisation du modulo.

Voici une première implémentation en C++ de notre application :

// Codage/décodage au moyen du chiffre de César
#include <iostream>
#include <string>
#include <algorithm>
#include <cmath>

using namespace std;

int modulo(int Dividende, int Diviseur);
int numeroDeLettre(char Letter);
char lettreDeNumero(int LetterNumber);
bool estUnCaractere(char Char);
string encodeCesar(string Phrase, int Shift);
string decodeCesar(string Phrase, int Shift);

// Programme principal
int main() {
    string Phrase;
    int Decalage = 0;

    // Saisie de la phrase et du décalage
    cout << "Phrase a coder : ";
    getline(cin, Phrase);

    // Converti la phrase en majuscules
    transform(Phrase.begin(), Phrase.end(), Phrase.begin(), ::toupper);

    cout << "Decalage : ";
    cin >> Decalage;

    // Codage et décodage
    string PhraseEncodee = encodeCesar(Phrase, Decalage);
    cout << "\nPhrase codee :  " << PhraseEncodee << "\n\n";

    return 0;
}

// Retourne le numéro de la lettre donnée en paramètre.
int numeroDeLettre(char Lettre) {
    return Lettre - 'A';
}

// Retourne la lettre correspondant au numéro donné en paramètre.
char lettreDeNumero(int NumeroDeLettre) {
    return NumeroDeLettre + 'A';
}

// Retourne un booléen indiquant si le caractère donné correspond à une
// lettre de l'alphabet.
// Par souci de simplification, les lettres accentuées sont ignorées.
bool estUnCaractere(char Caractere) {
    return Caractere >= 'A' && Caractere <= 'Z';
}

// Encode la chaîne passée en paramètre avec le décalage donné.
string encodeCesar(string Phrase, int Decalage) {
    string::iterator it = Phrase.begin();
    // Chaque caractère de la phrase est codé l'un après l'autre
    for(; it != Phrase.end(); it++) {
        if (estUnCaractere(*it)) {
            int NumeroDeLettre = numeroDeLettre(*it);
            int NumeroDeLettreDecalee = (NumeroDeLettre + Decalage) % 26;
            (*it) = lettreDeNumero(NumeroDeLettreDecalee);
        }
    }
    return Phrase;
}

Voici le résultat de ce petit programme :

Phrase a coder : COMMENT ALLEZ-VOUS ?
Decalage : 3

Phrase codee :  FRPPHQW DOOHC-YRXV ?

Press <RETURN> to close this window...

Le décodage, par contre, met en lumière la différence entre le modulo et le reste de la division entière. Si la lettre A (numéro 0) doit être décalée d’une position à gauche (-1), la lettre à obtenir est la lettre Z (numéro 25) et non pas le numéro -1, qui ne correspond à aucune lettre.

Dividende Diviseur Quotient Reste Modulo
25 26 0 25 25
26 26 0 0 0
0 26 0 0 0
-1 26 0 -1 25

C’est donc bel et bien le calcul du modulo qu’il faut utiliser et non pas celui du reste. En C++, il ne faut donc pas utiliser l’opérateur %, mais plutôt la fonction modulo() vue plus haut.

La fonction de décodage peut donc être écrite ainsi :

// Décode la chaîne passée en paramètre avec le décalage donné.
string decodeCesar(string Phrase, int Decalage) {
    string::iterator it = Phrase.begin();
    for(; it != Phrase.end(); it++) {
        if (estUnCaractere(*it)) {
            int NumeroDeLettreCodee = numeroDeLettre(*it);
            int NumeroDeLettreDecodee = modulo(NumeroDeLettreCodee - Decalage, 26);
            (*it) = lettreDeNumero(NumeroDeLettreDecodee);
        }
    }
    return Phrase;
}

Sources :

Wikipédia : modulo informatique

Wikipedia : modulo operation

The math forum : Mod function and Negative Numbers

Tags:, , ,
Posted in Développement | 1 Comment »

L’arrondi

Friday, October 22nd, 2010

Introduction

Un arrondi est nécessaire lorsqu’un nombre d’une certaine précision, doit être converti en un nombre d’une moindre précision.

Typiquement, un arrondi doit être effectué lorsqu’un nombre à virgule est converti en un nombre entier.

Cette notion peut sembler toute simple. Nous avons tous appris en cours de math qu’un nombre à virgule s’arrondi de la façon suivante :

  1. si la partie décimale est inférieure à 0.5, le nombre est arrondi vers le bas (par exemple 1.3 ≈ 1)
  2. si la partie décimale est supérieure ou égale à 0.5, le nombre est arrondi vers le haut (par exemple 1.6 ≈ 2 ou encore 1.5 ≈ 2)

Un premier doute s’installe lorsqu’il s’agit d’un nombre négatif. Un arrondi vers le bas correspond-il a un arrondi vers un nombre plus positif ou plus négatif ?

D’autre part, est-ce réellement la seule façon d’arrondir un nombre à virgule ? Y a-t-il une façon plus juste qu’une autre ?

Lors de l’écriture d’un programme qui manipule des nombres ayant à être arrondis, il est nécessaire de connaître comment une fonction d’arrondi réalise l’opération et quel sera le résultat obtenu.

Pour commencer, voyons les différentes façons d’arrondir un nombre à virgule (appelé également nombre réel).

Arrondi vers le bas (arrondi vers -∞)

Le nombre réel est arrondi vers l’entier inférieur.

3.4 ≈ 3

-3.4 ≈ -4

Arrondi vers le haut (arrondi vers +∞)

Le nombre réel est arrondi vers l’entier supérieur.

3.4 ≈ 4

-3.4 ≈ -3

Arrondi par troncature (vers zéro)

Le nombre réel est arrondi vers l’entier suivant le plus proche de zéro. Concrètement, la partie décimale du nombre réel est simplement retirée.

3.4 ≈ 3

-3.4 ≈ -3

Arrondi vers les infinis (par éloignement de zéro)

Le nombre réel est arrondi vers l’entier suivant s’éloignant le plus de zéro.

3.4 ≈ 4

-3.4 ≈ -4

Arrondi au plus proche

Le nombre réel est arrondi vers l’entier le plus proche du nombre réel.

3.4 ≈ 3

3.6 ≈ 4

-3.4 ≈ -3

– 3.6 ≈ -4

Cette dernière forme d’arrondi pose problème lorsque la partie décimale est exactement à mi-chemin entre deux nombre entiers (par exemple 3.5 ou -3.5).

Dans ce cas, il existe plusieurs façons d’arrondir :

Arrondi vers le bas (vers -∞)

3.5 ≈ 3

-3.5 ≈ -4

Arrondi vers le haut (vers +∞)

Cette méthode d’arrondi est également appelée arrondi arithmétique asymétrique.

3.5 ≈ 4

-3.5 ≈ -3

Arrondi vers zéro

3.5 ≈ 3

-3.5 ≈ 3

Arrondi vers les infinis

Cette méthode d’arrondi est celle qui est certainement la plus communément utilisée en arithmétique. On parle également d’arrondi arithmétique symétrique.

3.5 ≈ 4

-3.5 ≈ -4

Arrondi au pair le plus proche (arrondi bancaire)

Si la partie entière est impaire, le nombre arrondi sera le nombre pair le plus proche.

Si la partie entière est paire, elle correspond au nombre arrondi.

3.5 ≈ 4

2.5 ≈ 2

-3.5 ≈ -4

-2.5 ≈ -2

Cette méthode élimine le biais qui survient en cas d’arrondi systématique vers les infinis (ou vers zéro).

Arrondi à l’impair le plus proche

Si la partie entière est paire, le nombre arrondi sera le nombre impair le plus proche.

Si la partie entière est impaire, elle correspond au nombre arrondi.

3.5 ≈ 3

2.5 ≈ 3

-3.5 ≈ -3

-2.5 ≈ -3

Cette méthode d’arrondi est très rarement utilisée, sauf lorsqu’il est important que -0.5 et 0.5 ne soient pas arrondis à zéro.

Arrondi stochastique

C’est le hasard (uniformément réparti) qui détermine si le nombre sera arrondi vers l’entier supérieur ou inférieur.

Comme pour l’arrondi au pair le plus proche, cette méthode élimine le biais d’arrondi, mais introduit une notion de hasard qui rend la reproduction de calculs impossible.

Arrondi alterné

L’arrondi est alternativement fait vers l’entier supérieur puis vers l’entier inférieur.

Résumé

nombre -2.6 -2.5 -2.4 -1.6 -1.5 -1.4 -0.6 -0.5 -0.4 0.4 0.5 0.6 1.4 1.5 1.6 2.4 2.5 2.6
vers +∞ -2 -2 -2 -1 -1 -1 0 0 0 1 1 1 2 2 2 3 3 3
vers -∞ -3 -3 -3 -2 -2 -2 -1 -1 -1 0 0 0 1 1 1 2 2 2
troncature -2 -2 -2 -1 -1 -1 0 0 0 0 0 0 1 1 1 2 2 2
vers les ∞ -3 -3 -3 -2 -2 -2 -1 -1 -1 1 1 1 2 2 2 3 3 3
au plus proche vers +∞ -3 -2 -2 -2 -1 -1 -1 0 0 0 1 1 1 2 2 2 3 3
vers -∞ -3 -3 -2 -2 -2 -1 -1 -1 0 0 0 1 1 1 2 2 2 3
vers zéro -3 -2 -2 -2 -1 -1 -1 0 0 0 0 1 1 1 2 2 2 3
vers les ∞ -3 -3 -2 -2 -2 -1 -1 -1 0 0 1 1 1 2 2 2 3 3
pair -3 -2 -2 -2 -2 -1 -1 0 0 0 0 1 1 2 2 2 2 3
impair -3 -3 -2 -2 -1 -1 -1 -1 0 0 1 1 1 1 2 2 3 3
stochastique -3 -3 ou -2 -2 -2 -2 ou -1 -1 -1 -1 ou 0 0 0 0 ou 1 1 1 1 ou 2 2 2 2 ou 3 3
alterné -3 -3 (-∞) -2 -2 -1 (+∞) -1 -1 -1 (-∞) 0 0 1 (+∞) 1 1 1 (-∞) 2 2 3 (+∞) 3

Note : lorsque un nombre négatif est arrondi à zéro, certaines implémentations préservent le signe devant le zéro : -0.5 ≈ -0, afin de distinguer un arrondi à zéro provenant d’une nombre négatif, d’un arrondi provenant d’un nombre positif.

Fonctions courantes d’arrondi

Chaque langage (et chaque bibliothèque de fonctions) met à disposition un certain nombre de fonctions d’arrondi.

J’ai tenté de réunir dans un tableau les différentes façons d’arrondir un nombre réel ainsi que les différentes fonctions proposées par un langage ou une bibliothèque particulière.

Je m’en suis tenu aux langages que j’utilise couramment : C++ (avec les bibliothèques standards), C++ avec la bibliothèque Qt, VBS et Java. J’y ai ajouté Excel (et donc Keynote, qui implémente les mêmes fonctions), que j’utilise également régulièrement.

méthode\langage VBScript C++ C++ et cmath C++ Qt Java et java.lang.math Excel
vers +∞ ceil() ceil()
vers -∞ Int floor() floor() INT() ENT()
vers zéro
(troncature)		 Fix static_cast<int>() trunc() int() ROUNDDOWN() ARRONDI.INF()FLOOR() TRONQUE()
vers les ∞ ROUNDUP() ARRONDI.SUP()CEILING() PLAFOND()
au plus proche vers +∞ qRound round()
vers -∞
vers zéro
vers les ∞ FormatNumber1 round() ROUND() ARRONDI()
pair Round CByte CInt CLng rint() rint()
impair
stochastique
alterné

1Contrairement aux autres fonctions qui retournent un nombre, FormatNumber retourne une chaîne de caractères formatée selon certains paramètres donnés. Il reste néanmoins intéressant d’observer la méthode d’arrondi utilisé par cette fonction.

Ce tableau montre bien la confusion qui peut s’intaller : une fonction nommée Round va par exemple faire un arrondi au pair le plus proche en VBS, mais un arrondi arithmétique symétrique en C++ et avec Excel. La fonction équivalente en Java fera un arrondi arithmétique asymétrique, de même que la fonction qRound de Qt !

Sources :

Wikipedia : Rounding to integer

Wikipédia : Arrondi

Aide et support Microsoft : How To Implement Custom Rounding Procedures

Tags:, , , ,
Posted in Développement | 1 Comment »